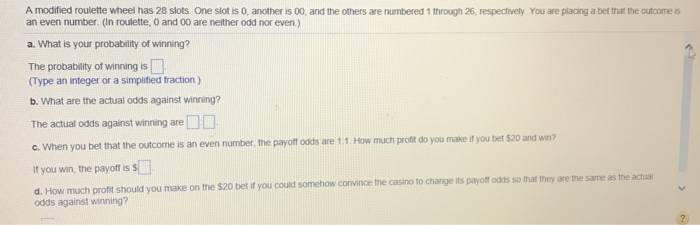
Roulette Probability Questions
In the game Roulette, a ball spins on a circular wheel that is divided into 38 arcs of equal lenght, numbered 00, 0, 1, 2, ... , 35, 36. The number on the arc on which the ball stops is the outcome of one play of the game. The numbers are also colored as follows:
1, 3, 5, 7, 9, 12, 14, 16, 18, 19, 21, 23, 25, 27, 30, 32, 34, 36 are red,
2, 4, 6, 8, 10, 11, 13, 15, 17, 20, 22, 24, 26, 28, 29, 31, 33, 35 are black,
0, 00 are green
Define the following events:
These are the values i got not sure if they are right
A: Outcome is an even number (0 and 00 are considered neither odd nor even) = 9/19
B: Outcome is a red number = 9/19
C: Outcome is a green number = 1/19
D: Outcome is a low number (1-18) = 9/19
(a) P(C) = 1/19
(b) P(AnB) = 4/19
(c) P(BuCuD) =
a and b are right i dont know how to get c
Thank you!
1, 3, 5, 7, 9, 12, 14, 16, 18, 19, 21, 23, 25, 27, 30, 32, 34, 36 are red,
2, 4, 6, 8, 10, 11, 13, 15, 17, 20, 22, 24, 26, 28, 29, 31, 33, 35 are black,
0, 00 are green
Define the following events:
These are the values i got not sure if they are right
A: Outcome is an even number (0 and 00 are considered neither odd nor even) = 9/19
B: Outcome is a red number = 9/19
C: Outcome is a green number = 1/19
D: Outcome is a low number (1-18) = 9/19
(a) P(C) = 1/19
(b) P(AnB) = 4/19
(c) P(BuCuD) =
a and b are right i dont know how to get c
Thank you!
Expressed as a number, the probability always exists between 0 and 1 – 0 would indicate that something is impossible to occur, while 1 would mean absolute certainty for the outcome. Even chances, for example, would be expressed as a 0.50 probability. In roulette, we have either 37 or 38 numbers in total, so these are all the possible outcomes. As the graph shows, the probability of seeing the same colour on consecutive spins of the roulette wheel more than halves (well, the ratio probability doubles) from one spin to the next. I stopped the graph at 6 trials/spins, as that was enough to highlight the trend and produce a prettier probability graph. Random roulette probabilities.
-
Probability Roulette Wheel Math
Probability Of Winning Roulette
make into disjoint sets and add up
(c) P(BuCuD) = P(B) + P(C) + P(LOW BLACK)
= (18+2+9)/38 = 29/38 <---------
(c) P(BuCuD) = P(B) + P(C) + P(LOW BLACK)
= (18+2+9)/38 = 29/38 <---------